フィボナッチ級数
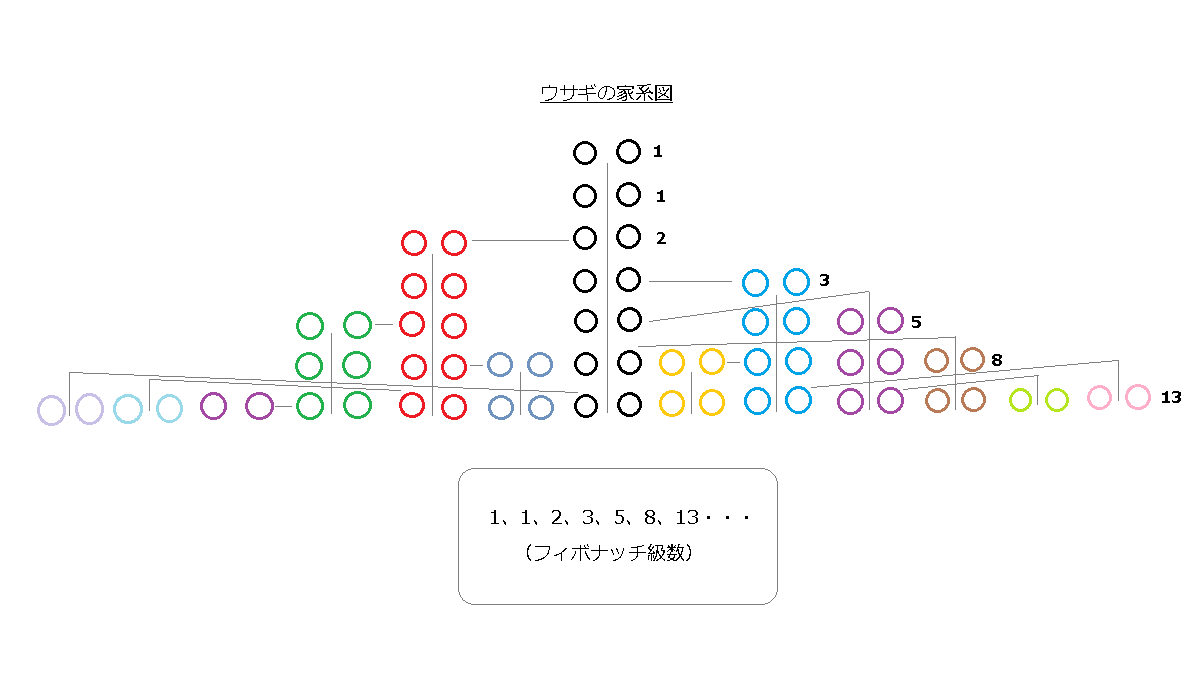
一度は目にしたことがあるかもしれませんが、「フィボナッチ級数」として知られている「ウサギのつがい」の図です。下手で申し訳ございません。あちこちで見ることはできるのですが、どうもイメージが沸きずらかったため自分で描いてみました。
スタートは1対のつがい(オスとメス)で、1ヶ月目はそのままの状態(増えない)、2ヶ月目から1対ずつ産みます。注意点として、1回産んだら終わりではなく、その後も何度も何度も1ヶ月毎に永遠に生み続けます。
そしてもう一つの注意点として、数の概念が違うということです。フィボナッチの「1」というのは、1対の1です。厳密に言うと、オスとメスの2匹で「1」なのです。フィボナッチの5は、オスとメスが5匹ずつ、10匹いることになります。単位が「つがい」なんですよね。
自分で描いていて不思議に思ったことが2つあります。一つは、どうして2ヶ月目からなのかということ。生まれて即子供が産めないというのはわかるのですが、3ヶ月目、4ヶ月目ではなく、どうして2ヶ月目なのかということです。
そしてもう一つは、産んだ子供が都合よくつがいになるのか、ということです。毎度毎度オスとメスの双子を産んでいるってことですから。たまにはオス一匹だけとか、三つ子であったりとか、メス2匹産んじゃって子供が産めないとかもあるでしょうに。
もちろん屁理屈を承知の上で言っているのですが、自分のお金を預けるわけですから、注意深くやりたいのです。エリオットの波動原理以上に、フィボナッチのほうがオカルト的要素が強いのではないかという、私自身の偏見もあります。
今現在当たり前に使われている数の概念的なものは、探せば意外と存在していて、たとえばアラビア数字であったり、10進法であったり、1時間は60分であったりなどのことです。そんななか、生物の本質的なものを探るというか数える概念としては、フィボナッチ級数のほうが適しているのかもしれないということは少し思いました。子孫繁栄の級数ですから、人間の本質を表しているというチャートの波であれば、フィボナッチ級数を適用させることは、強ち間違ってはいないのかもとも思うのです。
さて、上の図は画面の横幅上あれで一杯になってしまったのですが、つがいの数としては、「1,1,2,3,5,8,13,……(=フィボナッチ級数)」となりました。
「こうしたウサギの問題から提起されたフィボナッチ級数には多くの面白い性質があり、その構成要素の間にはほぼ一定の関係が存在する。」
これらの隣り合わせの数字を足していくと、次の数字になっています。「1+1=2、1+2=3、2+3=5、3+5=8、……」=「2,3,5,8,……」これもまたフィボナッチ数です。
数列
数学において数列(すうれつ、英: numerical sequence)とは、数が列になったもの (sequence of numbers) を言う。
ある数はそれ単独で興味深い性質や深い意味を持っているかもしれない。単独ではそれほど面白くはない数たちもまとめて考えると興味深い性質を持つかもしれない。数列を考える意識は後者に属する。
引用元:数列|ウィキペディア
級数
数学における級数 (きゅうすう、英: series) とは、ひと口に言えば数や関数など互いに足すことのできる数学的対象の列について考えられる無限項の和のことである。
引用元:級数|ウィキペディア
黄金比率
フィボナッチ数列
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …
前回学習しましたが、『厳密に言うと、これは「単なる数字」ではなく「数列」である。』ということでした。「3」とか「21」というのは、単なるアラビア数字のひとつで、単体でもそれ以外の数字よりは意味はあるのでしょうが、どちらかというと組み合わせで使ってこそ威力を発揮するもののようです。少なくとも相場の世界では。
参考:フィボナッチ級数|ピサのレオナルド・フィボナッチの略歴
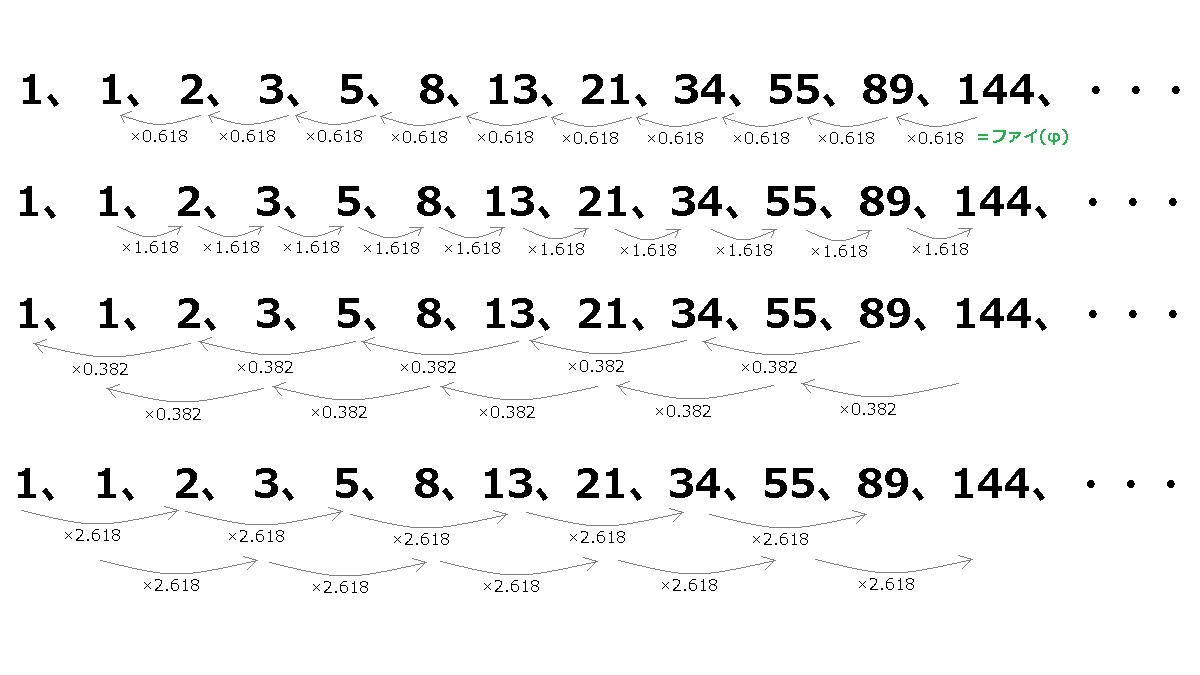
1つ前の小さな数字の比率≒0.618⇒ファイ(φ)0.618034…
(1つ前の数字÷次の数字)
1÷2=0.5、2÷3=0.6666…、3÷5=0.6、5÷8=0.625、8÷13=0.6153…、13÷21=0.6190…、21÷34=0.6174…、34÷55=0.6181…、55÷89=0.6179…
1つ後ろの大きな数字の比率≒1.618
(1つ後ろの数字÷前の数字)
2÷1=2、3÷2=1.5、5÷3=1.6666…、8÷5=1.6、13÷8=1.625、21÷13=1.6153…、34÷21=1.6190、55÷34=1.6176…、89÷55=1.6181…、144÷89=1.6179…
2つ前の小さな数字の比率≒0.382
(2つ前の数字÷今の数字)
1÷2=0.5、1÷3=0.3333…、2÷5=0.4、3÷8=0.375、5÷13=0.3846…、8÷21=0.3809…、13÷34=0.3823…、21÷55=0.3818…、34÷89=0.3820…
2つ後ろの大きな数字の比率≒2.618
(2つ後ろの数字÷今の数字)
2÷1=2、3÷1=3、5÷2=2.5、8÷3=2.6666…、13÷5=2.6、21÷8=2.625、34÷13=2.6153…、55÷21=2.6190…、89÷34=2.6176…、144÷55=2.6181…
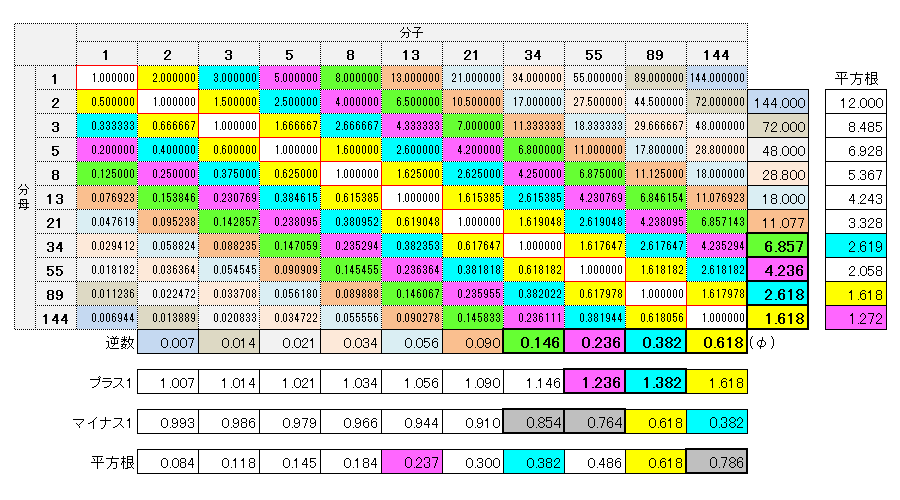
1+ファイ(φ)=1÷ファイ(φ)
「1+0.618=1÷0.618」:こうした性質を持つただ1つの数である。
フィボナッチ数は無限にありますが、結局どれが一番大切かというと、ファイの0.618でしょう(数というよりは比率ですが)。0.618さえ覚えておけば、あとは応用できると思います。
波動原理の中で「5」は最も重要な数字である。
5の平方根は、ファイに対する数学的なカギとなっている。
1.618(または0.618):黄金比率、中庸
「1:0.618034」の比率は、見た目にも、耳に対する響きも良く、生物学、音楽、芸術、建築などに広く取り入れられている。
- トランプカード
- パルテノン神殿
- ヒマワリ
- カタツムリの殻
- ギリシャの壺
- 宇宙の渦巻き状の星雲など
自然界においてフィボナッチ数と黄金らせんが連続して起こることは、芸術においてなぜ1:0.618034の比率が非常に心地良いのかを正確に説明している。人間は中庸に基づく芸術に生命のイメージを見ている。
自然は、最も繊細な構成要素や最も進歩的なパターンにおいて黄金比率を使っている。
- 脳の微小管
- DNA分子
- 惑星までの距離や期間
- 体の5つの腕や足やしっぽ→(2本の腕)→腕は3つの部分で成立→5本の指→指は3つの部位⇒「5-3-5-3」:波動の原理を示唆している。
まとめ
今回の内容は、書籍(「エリオット波動入門」)では8ページほどなのですが、かなり端折りました。正直申しますと、のめり込むのが怖いです。たくさんの事例を挙げられて、凄いという感嘆の声を上げたくもなるのですが・・・。人間のDNAなど極小のものから、惑星など巨大なものまでですから、なくもないという気はします。
とりあえず覚えておきたいのは、ファイの0.618、黄金比率の1.618、予備として0.382、2.618くらいでしょうか。他、波動原理では「5」が一番重要な数字であるということです。

コメント