エリオットの最初のフィボナッチ適用例
「ロバート・レアの本が出版されてから数年後に、エリオットは自身で最初に比率分析が適応可能であることを知った」そうで、その最初に気付いたのが以下の2つの衝撃波ということです。
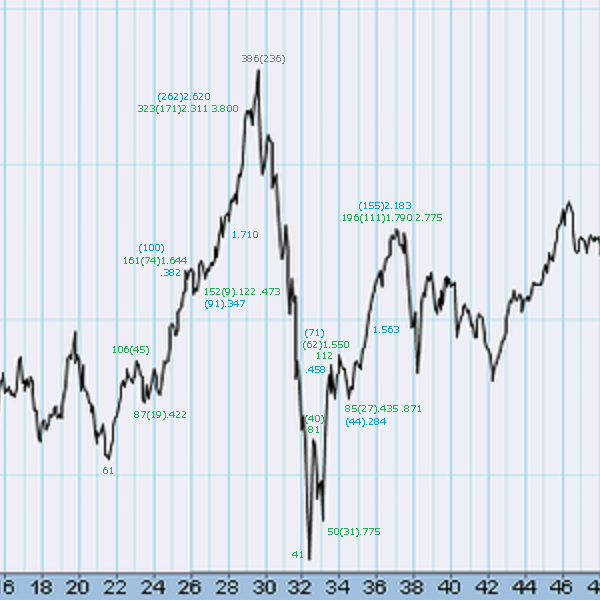
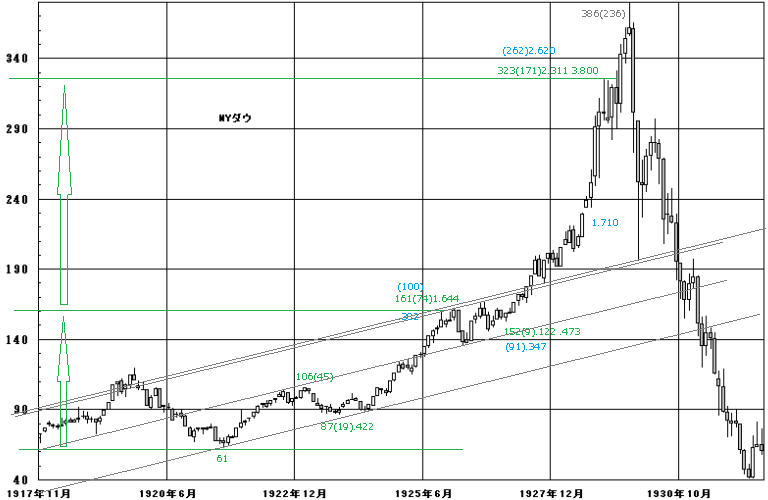
1920～1930年代、NYダウ
エリオットの最初の比率分析
画像引用元：Dow Jones Industrial Average – 1900-Present｜StockCharts
「(第1波+第3波)：第5波」＝「0.618：1」、になっているということです。ちなみに上のチャートは半対数目盛のものであるため、形状は当てになりません。
1921年、衝撃波のフィボナッチ
最初の衝撃波の、こちらは普通目盛のチャートです。第3波のトップで、大凡「0.382：0.618」の黄金比率で分割できます。
ただひとつ疑問に感じたのが、第1波と第3波の関係性も1.644なのですよね。第3波を延長波と解することもできるのではないかと思ってしまいます。このあたりは臨機応変な対応が必要なのでしょう。
第5波のトップは、実際の高値ではなく、オーソドックスな天井にラインを引いているつもりです。エリオットは、トップは拡大型フラットという解釈らしいのですが、著者は反論しています。
参考：イレギュラーなトップ（Irregular Top）｜用語の補足説明
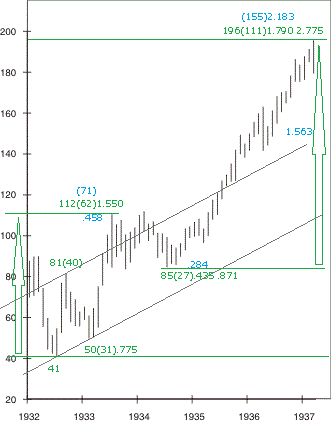
1932年、衝撃波のフィボナッチ
2つ目の衝撃波の普通目盛のチャートです。最初の衝撃波とほぼ同じ仕組みです。第5波が延長しているタイプの衝撃波が、2連続で出現したということになります。
第5波延長時のパターン
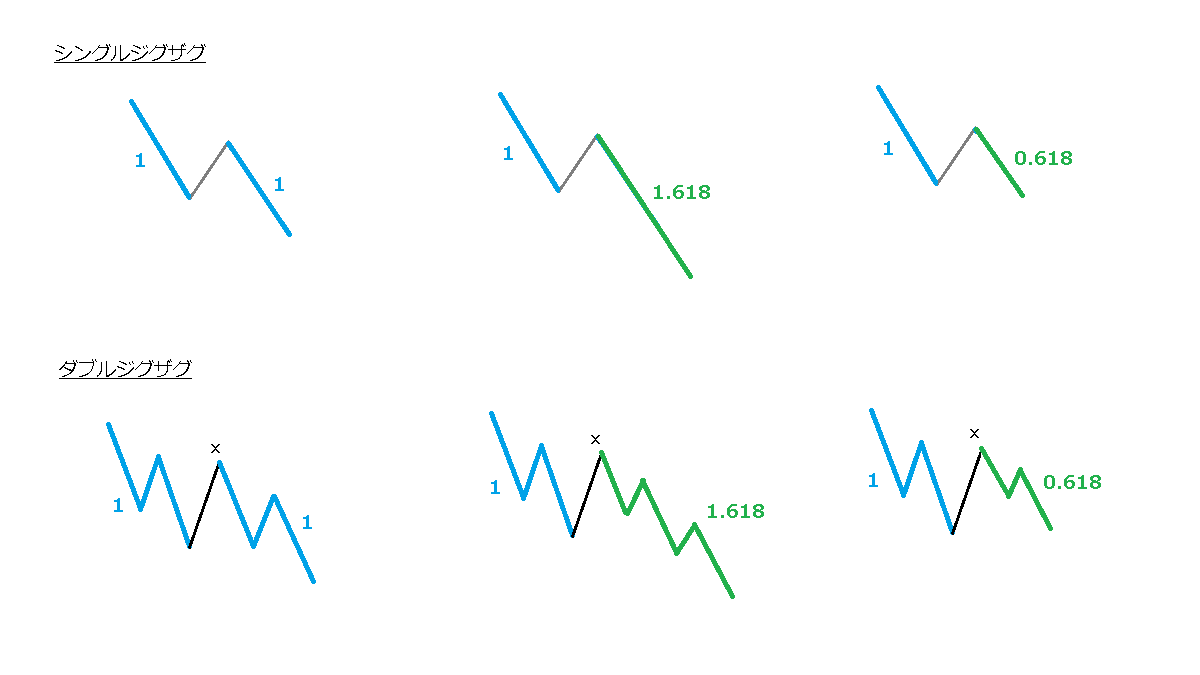
少しもやもやとするものがあり、上図を描いてみました。上の2つの第5波の延長の例ですが、フィボナッチの計算の仕方が微妙に違っています。衝撃波のフィボナッチの適用の仕方としては、波の比較と波の分割がありますが、このあたりは厳密なものではありません。第4波の価格帯ということで、トップであったりボトムであったり、比較であったり分割であったりします。私なりの覚え方が上の3パターンです。
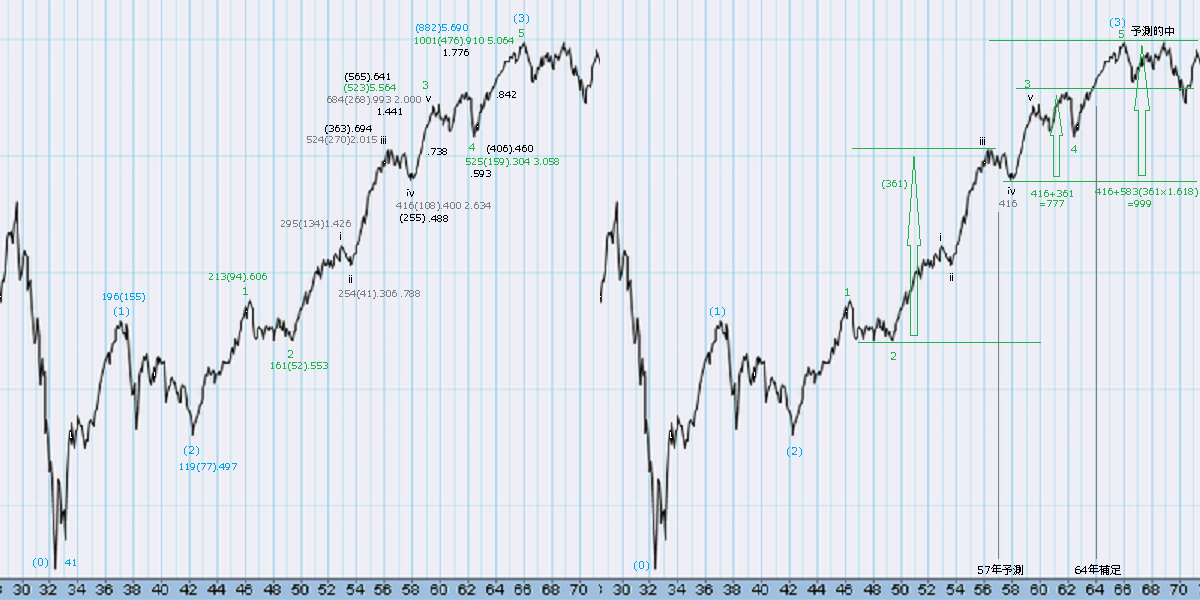
ボルトンの予測
衝撃波の第5波の予測
ボルトンの予測
A・ハミルトン・ボルトンの予測がほぼ的中した例です。これも半対数目盛りのチャートのため、数値と形状は一致していません。
ボルトンの予測、イメージ図
半対数目盛のチャートだとイメージしずらいため、上図を描いてみました。
今回は第ⅲ波が第ⅰ波のほぼ倍ですから、先のエリオットの例と同じく、第ⅲ波が延長波なのではないかと予測したくなりますし、だとすれば第ⅴ波の予測としては、波の均等性により第ⅰ波と同等の波の出現を予測したくなります。実際は、その延長波っぽい第ⅲ波と同等の波が出現しました。
しかしボルトンは、第ⅰ波と第ⅲ波を合計した数値の1.618倍（またはその合計した数値）まで伸びると予測しています。先のエリオットの2つの例と同じアプローチです。
延長波は延長波として考慮すべきだとは思うのですが、第1波と第3波の合計が第5波と何某かのフィボナッチ比率の関係になっているということだと思います。ラべリングと一致していはいないのですが、最終的には確かにボルトンの予測は当たっています。
波形の分析は比率関係の重要性に勝る。
これはボルトンの考えであり、著者も同意しています。
- まず最初にどの地点から計測するのかを決めるうえで、エリオット波動のカウントと符号の表記法をよく理解して適用することが不可欠である。
- そのときに信頼できるのは、一般にはオーソドックスなパターンの終了水準に基づく波の長さの比率であって、非オーソドックスな高値や安値ではない。
あれもこれもと数値を取り出すと収拾がつかなくなってしまいます。基本はオーソドックスな天井、底と覚えておきます。
参考：オーソドックスな天井と底
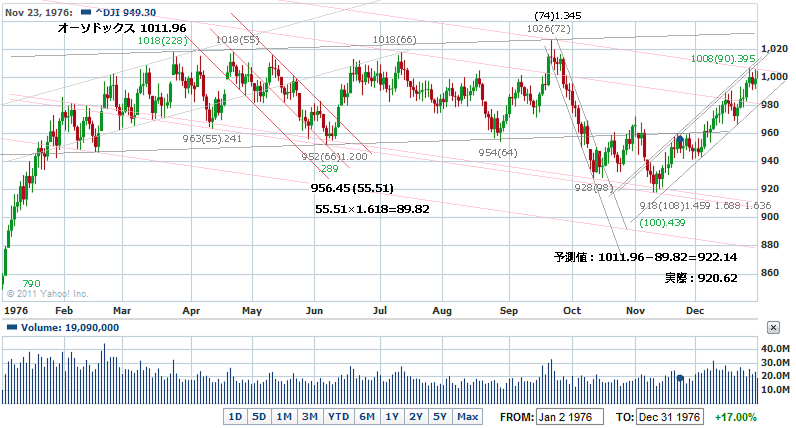
修正波の下限の予測
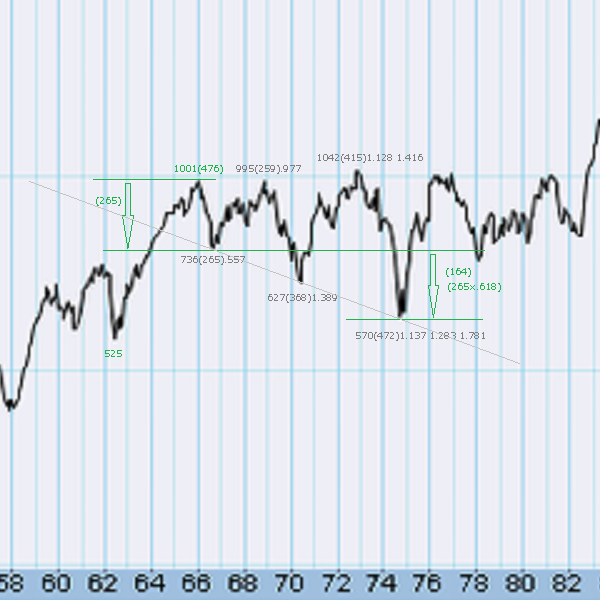
ボルトンの安値の予測
波動原理におけるフィボナッチというのは、ラべリングよりも、まずは波形を見ることが大切だと思っています。拡大型トライアングルとしてみれば、一応は教科書どおりの動きになっています。これもオーソドックスな天井を使用しています。
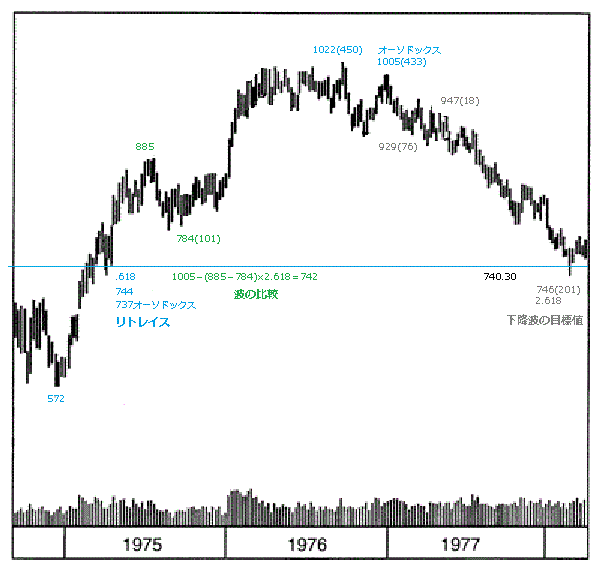
プレクターの予測
1978年、NYダウ
1978年、プレクターの安値の予測
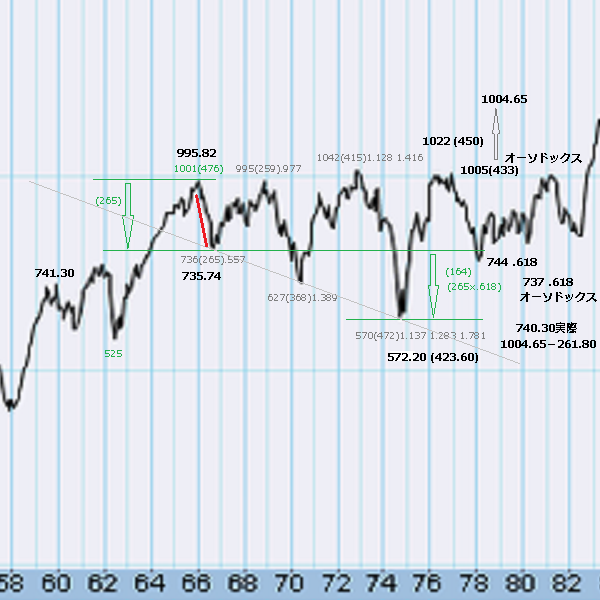
1976年、プレクターの安値の予測
先のボルトンの予測と全く同じアプローチです。これもまたオーソドックスな天井を使っています。このような波形での0.618、1.618というフィボナッチ比率は、相当堅そうです。
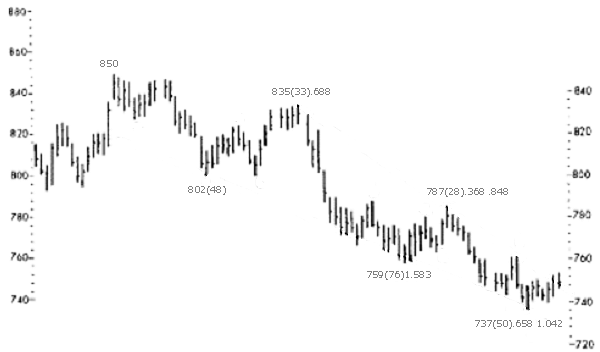
1978年、プレクターの安値の予測-1
画像引用元：[Article] A Track Record of WP Application to the Stock Market – Part II｜SOCIONOMICS
この波のカウントは、結果的には、上昇波がトライアングルのB波、その後の下降波がジグザグのC波の副次的なa波なのではないかと解釈しています。ただその上昇波ですが、完成するまでは候補を2つ挙げており、5波動の上昇波という見方もしています。
リトレイスの0.618は、5波動であればガイドラインどおりなのですが、3波動のジグザグとしては違和感を覚えます。5波動としても受け入れられる3波動ですから、このような初期に延長する波形の場合には、副次的な第2波のボトムは、その後において何某かの重要ポイントになるかもしれないと覚えておきます。
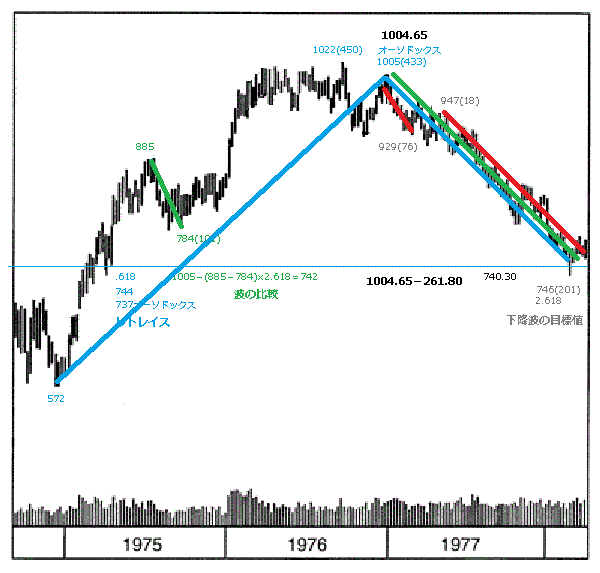
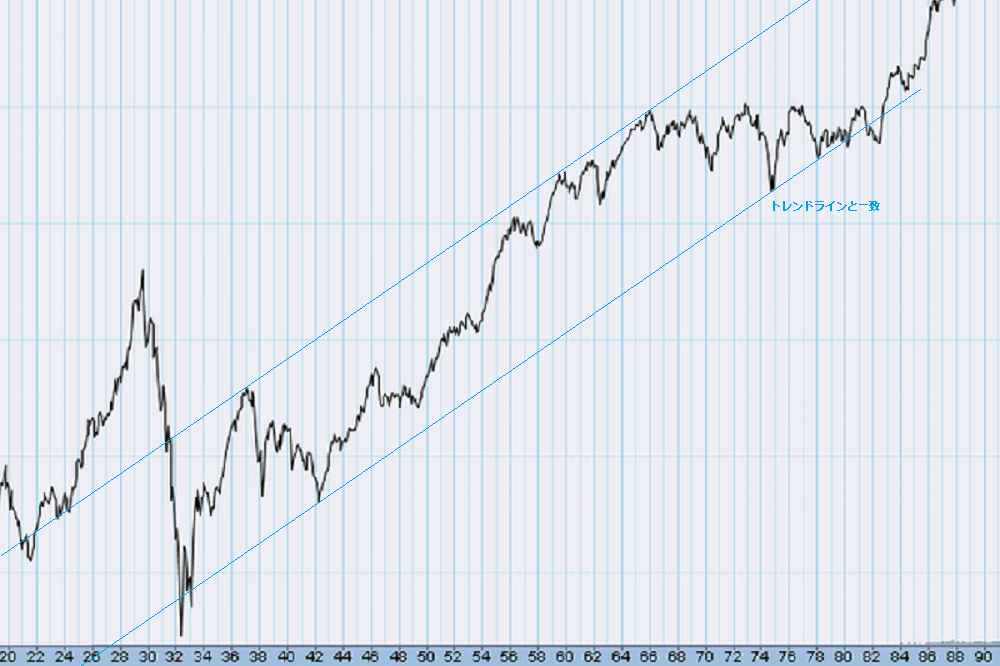
1978年、プレクターの安値の予測-2
1978年、プレクターの安値の予測-3
トレンドラインとも一致しているということです。
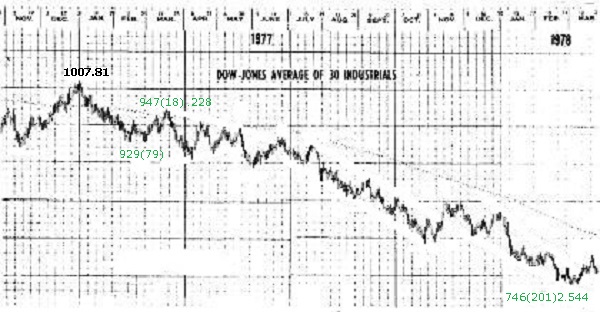
1978年、プレクターの安値の予測-4
1978年、プレクターの安値の予測-5
画像引用元：[Article] A Track Record of WP Application to the Stock Market – Part II｜SOCIONOMICS
1978年、プレクターの安値の予測-イメージ図
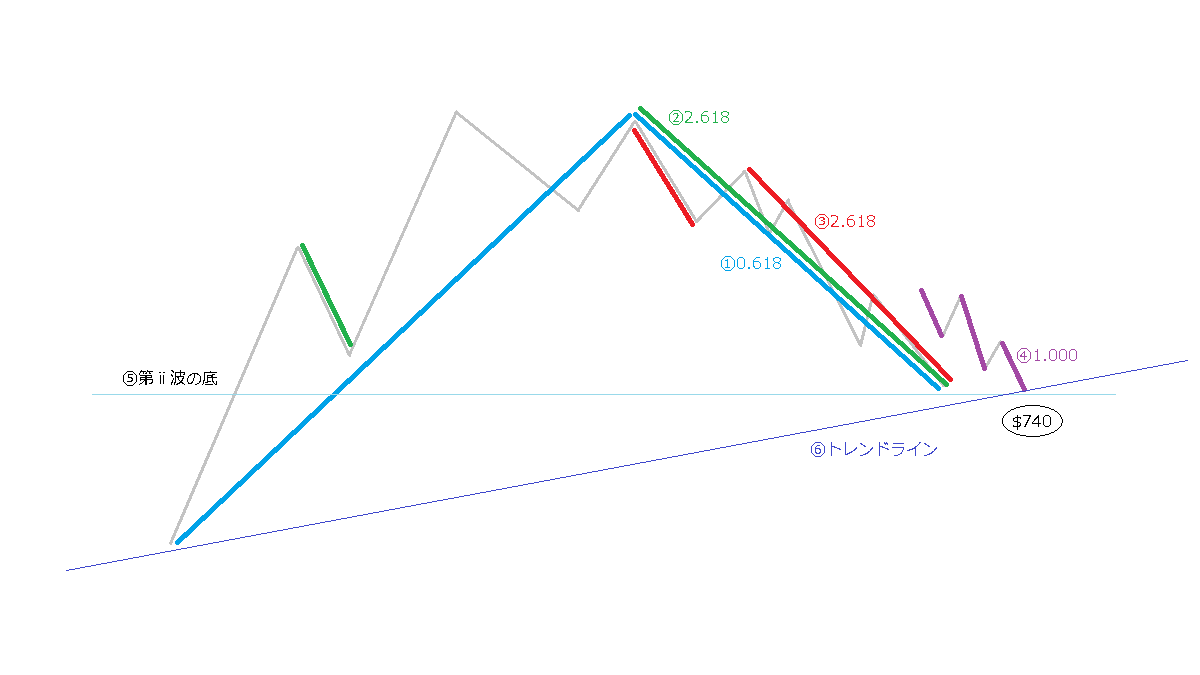
上図は、ここまでの1978年のプレクターの予測の仕方をイメージして描いたものです。ざっくりと6つの条件を提示しているようです。
- 大きな段階の波形のリトレイス：0.618
- 同方向の直前の波との比較：2.618
- 進行中のジグザグのA波とC波の比較：2.618
- 最後のダイアゴナルの副次波の比較：1.000
- 第1波が延長した場合の副次的な第ⅱ波の底
- トレンドラインが一致
エリオットの波動原理を使っての予測に関しては、このようなアプローチが最終形になるのだと思います。フィボナッチを幾つか掛け合せるのです。勿論前提条件として、ここまで学習した波形に関するルールやガイドラインをフル活用した上での予測です。エリオット、ボルトン、プレクター、ここに登場した3人のアプローチは、基本的には皆同じに見えます。
プレクターのフィボナッチ
プレクターはエリオットのより伝統的な株価予測法に加えて、時間と価格の両面で数学的な波の要因をリサーチし始めた。その結果以下のことがわかった。
- 推進波：整数倍
- 修正波：フィボナッチ比率の倍数
前回まで学習したフィボナッチについては、整数倍というのはありませんでした。推進波に限っては整数倍の可能性も考慮しておくべきでしょう。考えてみれば、0.618、1.618などはフィボナッチ比率であって、1、2、3、5、8などはフィボナッチ数なのですよね。そういえばフィボナッチ数を使った分析も登場していました。
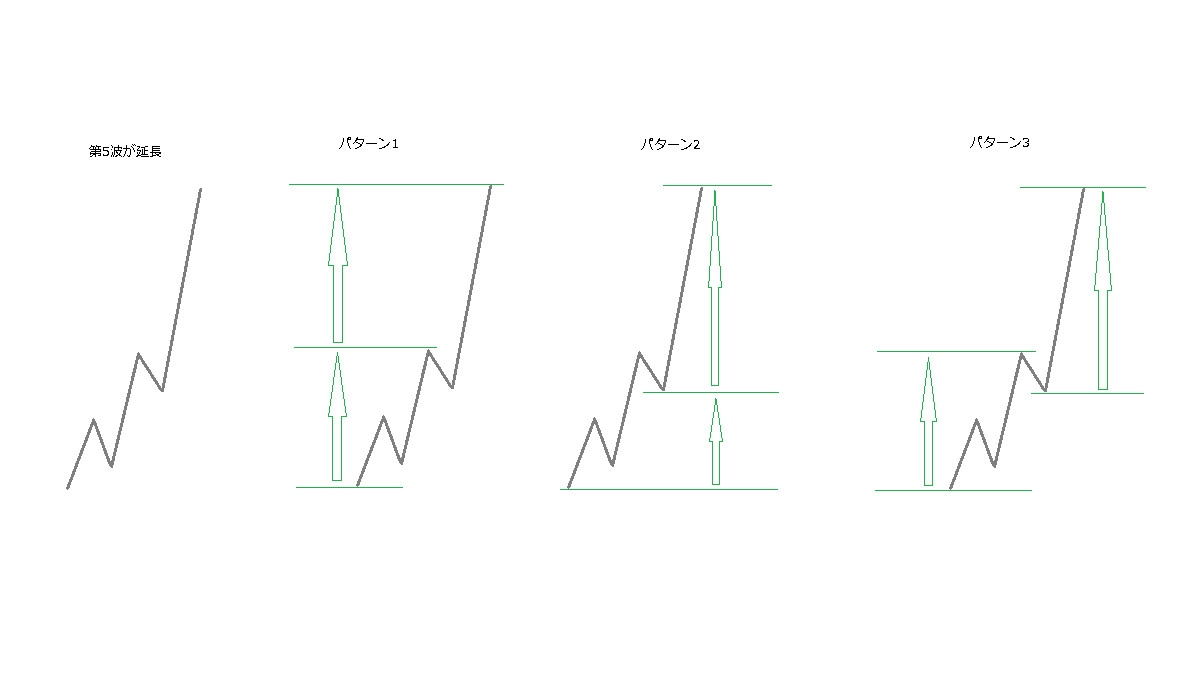
コメント