波動原理の構成におけるフィボナッチ数学
色々な波動パターンのフィボナッチ級数的な構成
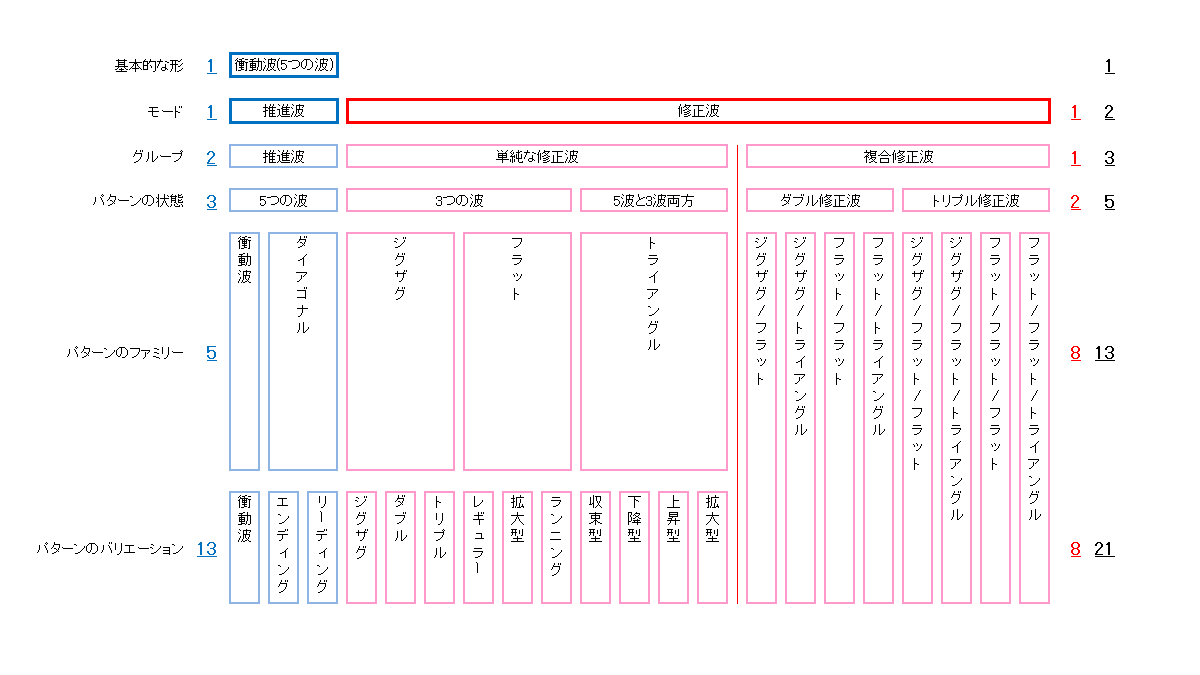
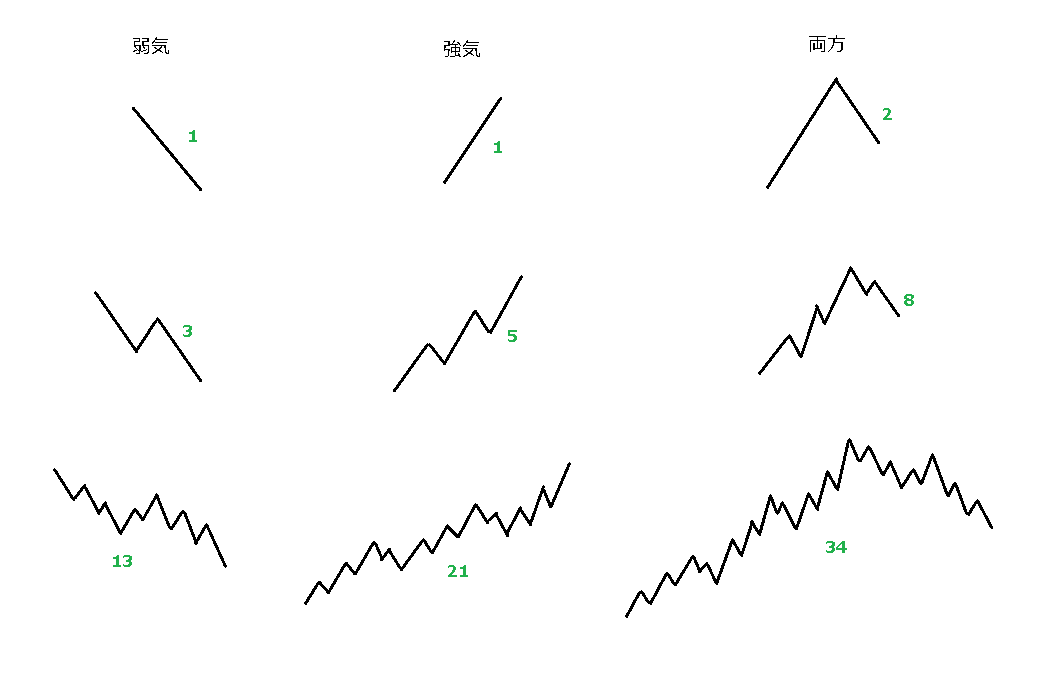
『エリオット波動の整然とした複合的な構成でさえも、フィボナッチ級数を反映している。』 上図は、書籍（「エリオット波動入門」）に載っている図（ツリー状）を真似したものです。若干違うのですが、恐らくこういうことだろうと。
横に記載してある青とか赤とかの数字が、フィボナッチ級数になっているということです。 前回の「らせん的な株式相場におけるフィボナッチ」と同様、こじつけのような気もしなくもありません。フィボナッチ級数を基に、そこに波動パターンを当てはめていったような気がしてしまいます。「フィボナッチありき」の波動原理ということです。
逆に、例えば上図のように各波動パターンを書き出していったら、偶然フィボナッチ級数に一致していたとなれば、それこそ凄いことだと思うのですが。私はまだ多少疑いの目で見てしまっています。
ちなみに、許容できる範囲内で波のバリエーションを意図的に変更しても良いそうです。複合型の修正波の、出現する順番を替えるとかでしょうか。
「フィボナッチ級数」： 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …
ファイと加算級数
株式相場の動きは、黄金比率に支配されている。
「フィボナッチ数そのもの」でさえも、しばしば単なる偶然とはいえない頻度でマーケットの統計に出現するし、波動原理の壮大なコンセプトにおいては何らかの理論的な重要性を持っているが・・・。しかし、成長パターンの基本的なカギとなるのが「フィボナッチ比率」であることを理解すべきである。
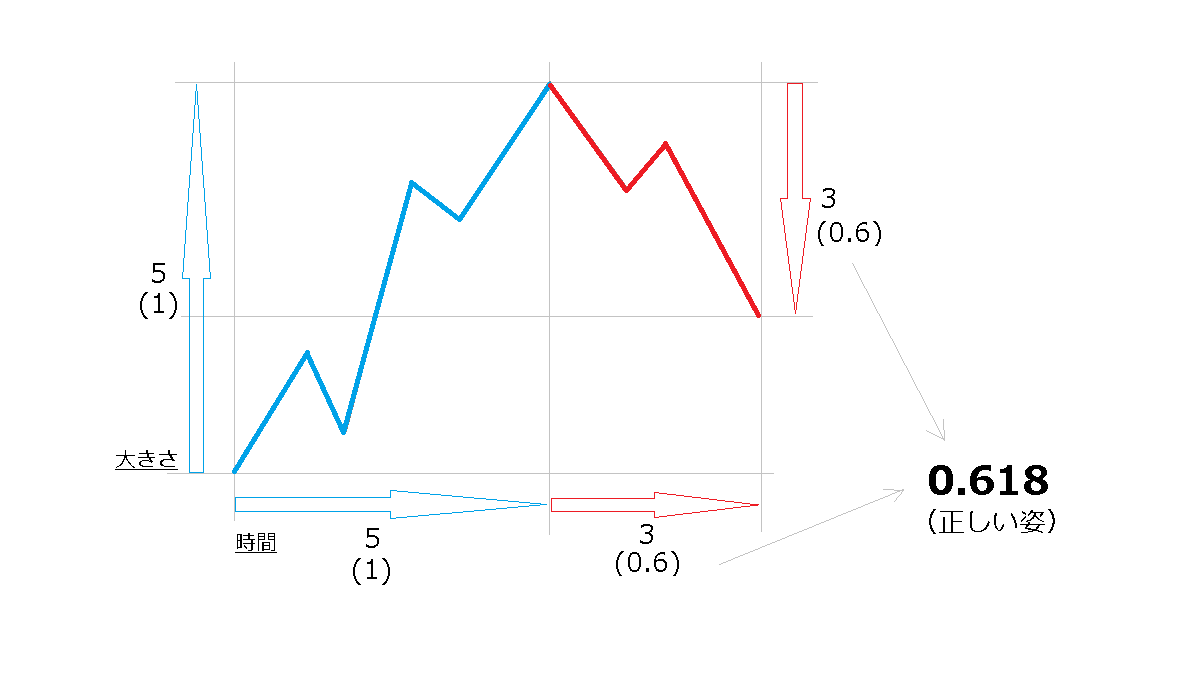
フィボナッチといっても、「フィボナッチ数」と「フィボナッチ比率」の大きく2種類あります。3波、5波などの3、5はフィボナッチ数ですが、それよりも0.618などの比率のほうが圧倒的に重要だということです。
3、5は、3、5そのものにしか使えませんが、0.618であれば、適用しようとすればどんな場面でも適用できます。使える範囲が全然違いますよね。
ファイと加算級数
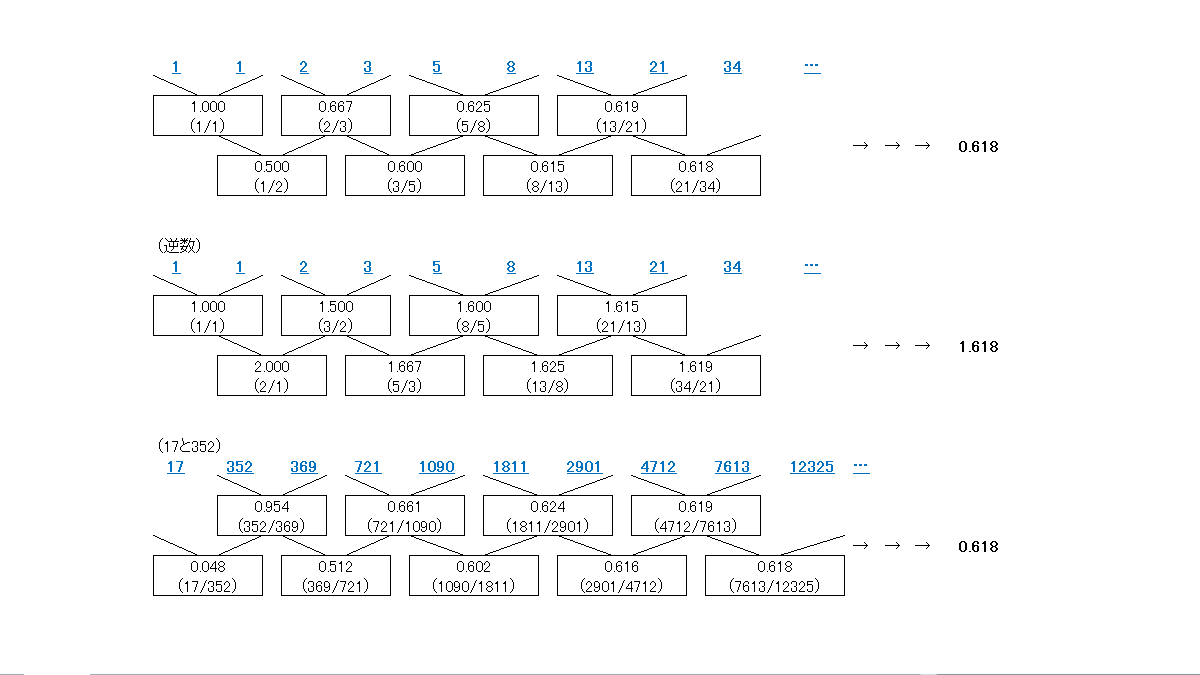
「どのような2つの数でこの数列が始まろうとも、フィボナッチ比率はこうした加算級数の結果として生じる。」
上図ですが、一番下の「17」と「352」はフィボナッチ数ではありません。それにも拘わらず、足していき、それらを割っていくと、0.618に近づいていくということです。
株式相場は世の中で最も如実に群集心理を反映している。
「群集行動」も紛れもなく研究し定義できる法則と繋がっているという点で、「株式相場」もその例外ではない。最も簡潔にこの原理を表現すると、それは単純な数学的な記述、すなわち1.618の比率となる。
コメント